La estimación de la eficacia biológica es muy diferente cuando se consideran caracteres cuantitativos que cuando estos caracteres son cualitativos. De hecho se han propuesto múltiples métodos para estimar la eficacia de caracteres cuantitativos a partir de diferentes diseños experimentales (revisado en Endler, 1986; Henshaw et al. 2018). En este curso de introducción vamos a explicar varios de estos métodos, que en el fondo son variantes de un mismo método.
Diferencial de selección
Si pretendemos medir la selección mediante un diseño transversal, es decir, cuando se disponen de medidas de un carácter antes y después de que actúe la selección (ver capítulo 1 de este tema), necesitaremos, por tanto, conocer la distribución de dicho carácter antes y después de que actúe la selección (ver Figura 1). Esta estrategia se viene aplicando de forma general durante la mejora genética de las especies domesticadas de plantas y animales (Caballero 2017), donde los ejemplares que se van a reproducir lo hacen con el permiso del mejorador (ganadero o agricultor), y tenemos que hablar, por lo tanto, de selección artificial, si bien la lógica y la práctica es similar al de la selección natural. Vamos a ver el modelo más simple de selección, conocido como selección por truncación, donde el mejorador determina qué ejemplares se van a reproducir poniendo una barrera imaginaria (un valor determinado) en la distribución de un carácter (la línea vertical discontinua más larga en la Figura 1). A los ejemplares que posean un valor del carácter que esté a la izquierda de esa barrera, no se les permite reproducirse. Un ejemplo hipotético de selección natural sería cuando en una determinada población, todos los años se muriesen de frío aquellos ejemplares que no llegaran a una cantidad determinada de tejido adiposo subcutáneo. Esa cantidad sería la barrera (ver más abajo el estudio de los Grant). La fuerza que tiene la selección en ese proceso se puede estimar mediante el diferencial de selección (S), que es la diferencia entre la media del valor del carácter en los individuos seleccionados por la selección natural y la media del valor del carácter en la población. En las figuras 1B y 1C, el valor de S está representado por la longitud del segmento que separa ambas líneas verticales, que es mayor en la figura 1B. El S es una estima realista cuando la selección es por truncación, es decir, cuando la eficacia de los individuos para el carácter en cuestión es de todo (se reproduce) o nada (no se reproduce).

Covarianza
Sin embargo, lo habitual es que las eficacias biológicas de los ejemplares que portan cierto carácter no sean discretas sino que covaríen con el carácter. Es decir la eficacia no es del todo o nada sino que puede presentar infinitos valores comprendidos entre el máximo y el mínimo posible. En vez de S, en este caso conviene entonces utilizar alguna medida estadística de la eficacia biológica más eficiente como puede ser la covarianza, que permite estimar la magnitud (entre -infinito e infinito) de la asociación entre el carácter y la eficacia biológica asociada al portador del mismo. Veamos un ejemplo práctico de cómo se usan las covarianzas y cómo se interpretan. En la Tabla 1 se presenta la relación entre dos variables (llamadas X e Y) en 3 escenarios diferentes. Estas mismas variables se pueden representar gráficamente mediante gráficos de dispersión (Figura 2; ver también la figura 3).
| Escenario 1 | Escenario 2 | Escenario 3 | ||||
| Casos | X | Y | X | Y | X | Y |
| C1 | 1 | 3 | 1 | 2 | 1 | 6 |
| C2 | 2 | 4 | 2 | 2 | 2 | 6 |
| C3 | 3 | 4 | 3 | 4 | 3 | 4 |
| C4 | 4 | 3 | 4 | 4 | 4 | 4 |
| C5 | 5 | 3 | 5 | 6 | 5 | 2 |
| C6 | 6 | 4 | 6 | 6 | 6 | 2 |
| Covarianza | 0.083333333 | 2.666666667 | -2.666666667 | |||
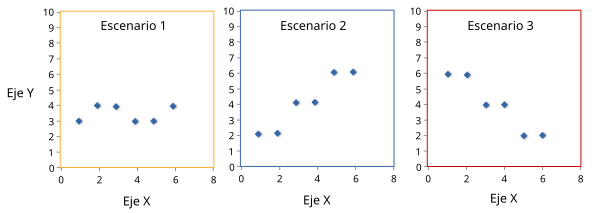

El tipo de relación entre el carácter (X) y su eficacia (Y) tiene obvias implicaciones evolutivas. Así en el escenario 2 esperaríamos que el valor del carácter X (asumiendo cierta base genética para el mismo) aumentase su media con el tiempo en la población, como siempre asumiendo que la eficacia se mantiene constante en el tiempo, y que otros factores evolutivos (migración, deriva genética o mutación) no afectan a la población de forma importante. Obviamente esperaríamos el efecto contrario en el escenario 3, una reducción paulatina del valor del carácter X en la población. Una forma simplificada de medir la asociación entre el carácter y su eficacia es calcular su covarianza, que como ya dijimos es la forma de estudiar el equivalente a S cuando las eficacias no son 0 o 1. La fórmula de la covarianza se presenta en la Figura 3, y se puede programar fácilmente su cálculo para los datos de la Tabla 1 en cualquier hoja de cálculo. Los valores de la covarianza en cada escenario se dan en la última fila de la Tabla 1. Vemos por lo tanto que una covarianza positiva nos indica que la eficacia tiende a aumentar al aumentar los valores del carácter y lo contrario cuando es negativa.
Coeficiente de regresión
Otra forma, muy relacionada con los métodos anteriores, de expresar la relación entre un carácter cuantitativo y su eficacia es mediante una recta de regresión. Probablemente este método es el más utilizado hoy en día para estimar la fuerza de la selección en experimentos de campo (ver formalización del método en Arnold y Wade 1984). El análisis de regresión (lineal y univariable) se utiliza cuando pretendemos predecir los valores de una determinada variable en función de otra. Usando nuestro ejemplo anterior pretendemos usar un carácter cuantitativo determinado (X) para predecir los resultados de otra variable como es la eficacia biológica (Y). Así, la recta de regresión lineal de X sobre Y se expresa en la Figura 4 para el escenario 2 (ver Figuras 1 y 2). La recta visualizada en la Figura 4 se obtiene al resolver la ecuación de regresión, que cuando es lineal sólo depende de 2 parámetros “a” (el valor de intercepción de la recta en el eje Y; 0.8 en este caso) y “b” (el coeficiente de regresión, que es 0.91 en este caso). Para determinar los valores esperados de Y debemos aplicar la ecuación anterior para cada valor del eje X correspondiente.
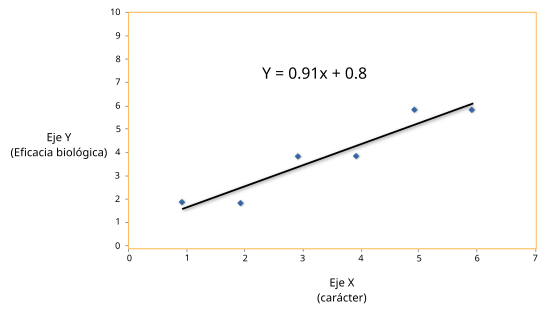
El coeficiente de regresión es igual a la covarianza dividida por la varianza del carácter X, y se puede considerar otra forma de medir la fuerza de la selección natural. La interpretación de un coeficiente de regresión es en principio bastante intuitiva. Así en el ejemplo de la Figura 4, b = 0.91, o lo que es lo mismo, para cada unidad que cambia la variable Y (pasa por ejemplo de 0 a 1, o de 1 a 2) la variable X cambia 0.91 unidades. Conviene resaltar que TODOS los estadísticos que hemos visto hasta ahora para estimar la importancia de la eficacia biológica en relación a cierto carácter cuantitativo (S, covarianza y coeficiente de regresión) comparten ciertas propiedades comunes. Por ejemplo, el signo no nos dice nada sobre la fuerza de la selección (fuerza de la eficacia biológica), sino que sólo nos indica la dirección de la relación, es decir, si el cambio en eficacia favorecerá a los valores más bajos del carácter (signo negativo) o a los más altos (signo positivo). Además, el valor absoluto no es desgraciadamente demasiado informativo porque está en función directa de la media del carácter estudiado. Así, para una selección fuerte o débil el valor puede ser más o menos alto en términos absolutos en función de que la media del carácter sea en unidades o decenas de unidades, etc. Esto en la práctica se corrige de múltiples formas. Por ejemplo mediante el empleo de estadísticos que dan la información estandarizada (expresada en unidades estándar de variación de cada carácter; el método más frecuente de estandarización es dividir el estadístico por la desviación típica). No obstante en un curso de iniciación como este no nos preocupamos por utilizar coeficientes estandarizados como la BETA de regresión o los gradientes de selección, etc, sino por entender y ser capaces de interpretar los estadísticos más básicos.
Significación de las medidas de selección
Otro aspecto práctico a considerar es que cuando se estima cualquiera de estos coeficientes, tan importante como la estima en sí, es saber si el valor observado es significativo o no. No lo es si los valores observados pudieran explicarse por azar, como consecuencia de efectos aleatorios de muestreo, etc. De nuevo, para la simplificación de un curso introductorio como este, ignoraremos todos los problemas de la validación estadística, los test de hipótesis y los intervalos de confianza de los estimadores, aunque cualquiera interesado en estos temas debería de revisar primero los conceptos claves en algún libro de estadística (por ejemplo Sokal y Rohlf, 1995). Finalmente la estimación de eficacias reales en caracteres cuantitativos en experimentos de campo pasa por el empleo de otros métodos de medida como la regresión lineal multivariable, regresión cuadrática, estima de los efectos sobre las interacciones, y otras complicaciones que están fuera de este curso introductorio (véase Arnold y Wade, 1984, para un desarrollo más específico de las posibilidades del método.
Podemos ver ahora un par de ejemplos reales de estimación de la selección natural (eficacia biológica) en caracteres cuantitativos. El primer ejemplo es el clásico experimento realizado por el conocido matrimonio de científicos (Grant y Grant 1989) sobre pinzones de cactus (Opuntia sp) en las islas galápagos (la especie Geospiza conisrostris; ver Tema Evidencias del Cambio Evolutivo, apartado evolución en laboratorio y en la naturaleza). Este estudio presenta datos que apoyan cómo la selección natural está modificando el tamaño del pico en esta especie. Esta especie presenta una gran variación en el grosor de su pico, y a su vez se ve afectada por cambios estacionales que imponen grandes mortalidades al limitar los frutos de los que se alimenta (la mortalidad aumenta en la estación seca). Estos científicos notaron que durante una serie de años se produjo un fenómeno climático mundial (el niño) que produjo un cambio del clima local, pasando del clima habitual húmedo (1983-1984) a un clima mucho más seco (1984-1985). Un clima más seco causa una disminución de las flores y los frutos de la planta Opuntia, de los que se alimenta, y creando así las condiciones para fuertes efectos selectivos. Los investigadores monitorizaron una población de pinzones y midieron todos sus picos, luego confirmaron en vistas posteriores cuales no habían sobrevivido durante los diferentes periodos de estudio, de forma que pudieron utilizar el método del coeficiente regresión para estudiar la relación entre el carácter y su eficacia, adjudicando un valor de eficacia biológica de 1 o 0 a los diferentes individuos, tal como hemos visto con anterioridad. Los resultados de dichas estimas de eficacia en los pinzones se presentan en la Tabla 2. Como se puede ver confirman un cambio en la selección natural con el cambio de clima, produciendo una mayor eficacia biológica hacia picos más cortos en la época húmeda (periodo 1983-1984; valores más grande en valor absoluto y negativo) y hacia valores más gruesos de pico en la época seca (periodo 1984-1985). Como ya hemos indicado en temas anteriores el signo sólo indica la dirección del cambio y no la magnitud de la selección actuando sobre el carácter.
| Periodo | Carácter | Sestandarizado | BETA±DT | Ntotal | NSupervivientes |
| Longitud | -0.24 | -0.22±0.08 | |||
| 1983-1984 | Grosor | -0.07 | -0.05±0.08 | 137 | 74 |
| Tarso | -0.1 | -0.02±0.07 | |||
| Longitud | 0.14 | -0.05±0.18 | |||
| 1984-1985 | Grosor | 0.31 | 0.37±0.19 | 74 | 29 |
| Tarso | 0.22 | 0.14±0.19 |
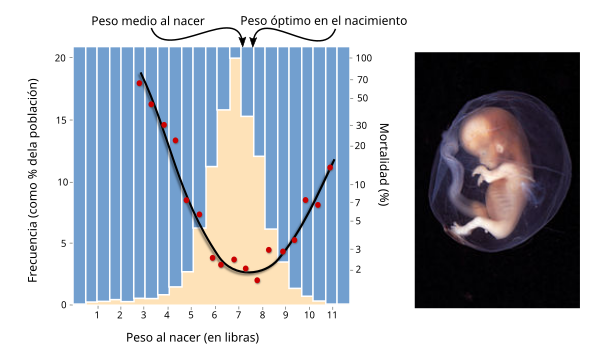
Por último podemos ver un ejemplo de selección actuando sobre un carácter cuantitativo en nuestra propia especie. Cavalli-Sforza y Bodmer (1971) recopilaron datos del peso al nacer en diferentes hospitales y representaron la distribución del carácter peso al nacer (Figura 5). El carácter, como la mayoría de caracteres, sigue una distribución en forma de campana (normal), y superpuesto a dicho carácter están las estimas de mortalidad asociadas a los mismos niños en esa misma población (línea roja). Como se puede observar la mortalidad de los niños al nacer aumenta al desviarse del óptimo de peso en la especie (de algo más de 7 libras en esta población). Para medir la selección en este carácter cuantitativo, peso, habría que usar otros modelos más complejos, ya que el uso de la regresión lineal no sería efectivo (véase que la distribución de mortalidad sigue una curva; Figura 5).
Para saber más:
Arnold S.J. y M. Wade. 1984. On the Measurement of Natural and Sexual Selection: Applications. Evolution, 38:720-734.
Caballero, A. 2017. Genética Cuantitativa. Editorial Síntesis. Madrid.
Cavalli-Sforza, L.L. y W.F. Bodmer. 1971. The genetics of human populations. Dover publications, inc., New York.
Endler, J.A. 1986. Natural selection in the wild. Princeton University Press, New Jersey.
Henshaw, J., Jennions, M. y L. Kruuk. 2018. How to quantify (the response to) sexual selection traits. Evolution, 72: 1904-1917.
Grant, B.R. y P.R. Grant. 1989. Natural selection in a population of Darwin’s finches. The American Naturalist, 133: 377-393.
Sokal, R.R. y F.J. Rohlf. 1995. Biometry. The principles and practice of statistics in Biological research. Third Edition., Freeman and Co., New York.