La selección natural ocurre en las poblaciones cuando se dan tres condiciones de forma simultánea: (1) que haya variación en algún carácter fenotípico; (2) que dicha variación sea heredable; y (3) que las distintas variantes de ese carácter fenotípico presenten una eficacia biológica diferentes las unas con respecto a las otras. Un aspecto clave para entender más en detalle el proceso de la selección natural es entender qué son los caracteres fenotípicos en los seres vivos. Una vez definidos, estaremos en disposición de medirlos.
Formalmente, un fenotipo es el conjunto de rasgos visibles que un individuo presenta como resultado de la interacción entre su genotipo y el medio ambiente. El genotipo es el conjunto de genes que un individuo posee y que en buena medida determina las características observables de dicho individuo. Un carácter fenotípico es, por tanto, cualquier rasgo asociado a un ser vivo (morfológico, anatómico, fisiológico, molecular, de comportamiento, etc.) resultado de la expresión de sus genes en un ambiente determinado. No todos los caracteres fenotípicos tienen la misma naturaleza, sino que se pueden agrupar en dos grandes categorías que condicionan la forma en la que los estudiamos: los caracteres discretos y los continuos, también denominados cualitativos y cuantitativos.
Caracteres fenotípicos discretos
Los caracteres fenotípicos discretos o cualitativos son aquellos que se presentan en forma de categorías discontinuas, es decir, que sus variantes se pueden agrupar por el observador en una serie de clases, de forma que cualquier ejemplar encontrado en el campo se puede adjudicar a alguna de estas clases. Se trata de una clasificación absoluta, de todo o nada. Un ejemplo típico de carácter discreto es el color: cualquier observador puede identificar de qué color es cada uno de los individuos que componen una población de una especie dada y agruparlos en función de este rasgo en categorías separadas (blanco, amarillo, naranja, marrón, etc.; ver Figura 1).
Otro ejemplo de caracteres fenotípicos discretos lo constituyen ciertos rasgos morfológicos o anatómicos que se expresan fundamentalmente en clases o categorías discontinuas y que se estudian con el calificativo de “mendelianos” en el contexto de la genética clásica. Ejemplos de esta clase de rasgos son la lisura o rugosidad de las semillas de la planta del guisante, o el tamaño de los ojos (normal o reducido) en las moscas del género Drosophila.

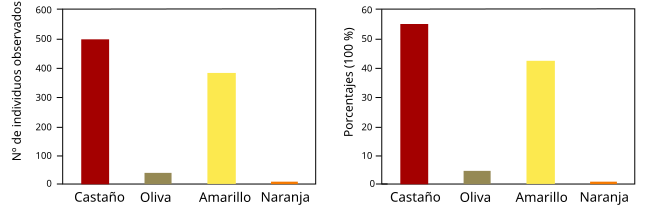
Estadísticamente, los caracteres discretos se describen en forma de frecuencias. Así, cuando queremos describir la variación cualitativa que existe en una población, en primer lugar establecemos una serie de clases y, posteriormente, contamos el número de individuos de cada clase. Por ejemplo, en la población del gasterópodo marino L. fabalis de Abelleira (Ría de Muros-Noia, Galicia, España), Rolán-Alvarez y Ekendahl (1996) observaron las frecuencias de colores representadas en la Tabla 1. Dichas cantidades se pueden expresar también en términos de probabilidad (o tanto por 1; el número observado en cada clase dividido por el total) o en forma de porcentaje (el valor anterior multiplicado por 100). Para expresar gráficamente este tipo de datos se suelen utilizar gráficos de barra como los que se muestran en la Figura 2.
| Colores | Castaño | Oliva | Amarillo | Naranja |
| Nº ejemplares observados | 492 | 36 | 377 | 1 |
| Probabilidad (1) | 0.543 | 0.04 | 0.416 | 0.001 |
| Porcentaje (100%) | 54.3 % | 4.0 % | 41.6 % | 0.1 % |
Caracteres fenotípicos continuos (cuantitativos)
A diferencia de los caracteres cualitativos, los caracteres fenotípicos cuantitativos, estadísticamente conocidos como caracteres continuos o de intervalo, pueden tomar cualquier valor dentro del intervalo de valores observado para las variantes del carácter. En otras palabras, los caracteres cuantitativos son aquellos que se clasifican en base a las categorías relativas de más y menos, y no tanto a las absolutas de presencia y ausencia, como en el caso de los caracteres discretos. Así pues, en este caso no se pueden hacer clases o categorías estancas para clasificar a los individuos, por lo que la mejor forma de expresar estos caracteres es mediante una función matemática que relacione la frecuencia esperada de los distintos valores de un carácter en la población con la distribución de los valores reales de éste. Estas funciones matemáticas se denominan funciones de probabilidad o de densidad, porque para cada valor particular del carácter nos da la probabilidad (o densidad) esperada de encontrarlo en la población original (véase la Figura 3).
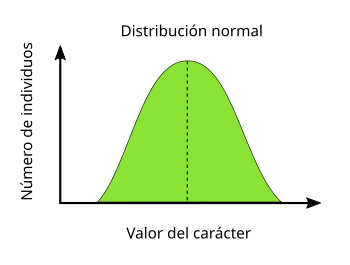
Existen infinitas funciones de probabilidad que podrían definir la relación entre los valores de un carácter continuo y su frecuencia en una población determinada. Quizás la más conocida es la función normal, que se describió por primera vez en el siglo XVIII por el matemático francés Abraham de Moivre y que fue desarrollada por el estadístico Carl F. Gauss en la primera mitad del siglo XIX. A pesar de su enorme utilidad para el estudio de los fenómenos biológicos, la función normal no captó la atención de los estudiosos de la evolución hasta que los investigadores agrupados en la escuela biométrica repararon a finales del siglo XIX que la mayoría de caracteres biológicos siguen de hecho una distribución normal. En la actualidad la distribución normal se considera la hipótesis nula de la distribución de cualquier carácter continuo en las poblaciones biológicas.
La función normal es una distribución de gran utilidad tanto para los estudios empíricos como los teóricos, ya que se trata de una distribución simétrica en forma de campana en la que todas las medidas de centralidad (media, moda y mediana) coinciden. Además, la distribución normal depende matemáticamente exclusivamente de dos parámetros, la media y la desviación típica, que se define como la raíz cuadrada de la varianza:
Media (µ) = (Σxi)/n
Varianza = (Σ(xi-µ)2)/n
Siendo xi el valor del carácter en cada individuo estudiado, µ la media del carácter en la población y n el número de individuos medidos para el carácter en cuestión (para una descripción más técnica entre caracteres discretos y continuos y sus consecuencias en los modelos y métodos estadísticos véase, por ejemplo, Sokal y Rohlf, 1995).
Para saber más:
Rolán-Alvarez, E. y A. Ekendahl (1996). Sexual selection and non-random mating for shell colour in a natural population of the marine snail Littorina mariae (Gastropoda: Prosobranchia). Genetica, 97: 39-46.
Sokal, R.R. y F.J. Rohlf (1995). Biometry. The principles and practice of statistics in Biological research. Third Edition., Freeman and Co., New York.Sokal, J.R. y J.R. Rohlf. 1885